Buktikan untuk setiap bilangan asli n.
Jika kamu sedang mencari artikel buktikan untuk setiap bilangan asli n terbaru, berarti kamu telah berada di website yang tepat. Yuk langsung aja kita simak ulasan buktikan untuk setiap bilangan asli n berikut ini.
1 Buktikan Pernyataan Be Descubre Como Resolverlo En Qanda From qanda.ai
Bukti Karena In interval bersarang maka InIn1 untuk semua n bilangan asli. Karena 0 habis dibagi 5 maka pernyataan bernilai benar asumsikan n 5 n habis dibagi 5 untuk setiap. N 4 4n 2 habis dibagi 3 untuk semua bilangan bulat lebih 2. N 4 4n 2 2 4 42 2 16 16 0.
Selanjutnya harus ditunjukkan bahwa pkl benar yaitu.
3 Buktikan dengan induksi matematika bahwa untuk semua bilangan asli n. 3 Buktikan dengan induksi matematika bahwa untuk semua bilangan asli n. Oleh karena itu himpunan A an. Nilai f2015 adalah. N 3 sehingga.
Source: qanda.ai
Nilai f2015 adalah. Sehingga diperoleh an bn a1 b1 untuk semua n. Langkah Basis Induksi Untuk n2 maka. Maka 1 5 1 0. Buktikan dengan Induksi Matematika untuk Semua Bilangan Asli n.
Misalkan pn menyatakan 1 1 2 3 1 2 n n n 1 p1 adalah 1 1 1 1 1 2 yaitu 1 1 jelas benar.
1 1 2 3 1 2 k k k benar. OSN SMA 2006 Pada segitiga ABC M titik tengah BCdan Gadalah titik berat segitiga ABC. Jawab Denisikan semesta dan predikat berikut. Bukti Karena In interval bersarang maka InIn1 untuk semua n bilangan asli.
Source: qanda.ai
Selanjutnya harus ditunjukkan bahwa pkl benar yaitu. 1 Buktikan dengan induksi matematika bahwa xn 1 habis dibagi x 1 n bilangan asli. 1 1 2 3 1 2 k k k benar. Bukti Karena In interval bersarang maka InIn1 untuk semua n bilangan asli.
Source: kompas.com
Jawab Denisikan semesta dan predikat berikut. PDF On Sep 30 2018 Herri Sulaiman and others published SIFAT-SIFAT KEKONVERGENAN PADA BARISAN FUNGSI REAL Find read. LMNAS SMP 2014 Tentukan nilai xyang memenuhi persamaan r 2014 x q 2014 x p 2014 2014 41. Untuk n 1 berlaku P1.
Source: qanda.ai
3 Buktikan dengan induksi matematika bahwa untuk semua bilangan asli n. Kita akan membuktikan soal ini dengan menggunakan induksi matematika. Untuk setiap bilangan asli n1 dan f1 2015. Dengan induksi matematik buktikan bahwa untuk setiap bilangan asli n berlaku 1 2 2 22 3 23 n 2n n 12n1 2.
Selanjutnya harus ditunjukkan bahwa pkl benar yaitu. Buktikan dengan induksi matematika pertidaksamaan 2n2n untuk setiap n bilangan asli. N 4 4n 2 habis dibagi 3 untuk semua bilangan bulat lebih 2. PDF On Sep 30 2018 Herri Sulaiman and others published SIFAT-SIFAT KEKONVERGENAN PADA BARISAN FUNGSI REAL Find read.
Untuk setiap bilangan asli n buktikan bahwa n² 5n 6 adalah bilangan genap bantuin kak.
1 Buktikan dengan induksi matematika bahwa xn 1 habis dibagi x 1 n bilangan asli. Selanjutnya harus ditunjukkan bahwa pkl benar yaitu. 1 Buktikan dengan induksi matematika bahwa xn 1 habis dibagi x 1 n bilangan asli. Secara umum dengan menggunakan induksi matematika dapat dibuktikan bahwa setiap bilangan asli n berlaku x2n1 1 1 1 1 1 3 5 2n1 2 2 2 2 deret geometri nsuku 1 1 1 2 1 1 n 4 34 2 1 14n. N 3 sehingga.
Source: id.pinterest.com
Jawab Denisikan semesta dan predikat berikut. Untuk setiap bilangan asli n buktikan bahwa n² 5n 6 adalah bilangan genap bantuin kak. Dalam Laten t S em antic Indexing kon sep dalam pertanyaan sama-sama baik unt uk setiap. Untuk n2 bilangan latex n3-n23-26 Dan 6 merupakan bilangan yang habis dibagi3. Soal Induksi Matematika Buktikan.
1 21 1 1211 2 P1. Penggunaan strategi pen gambilan tradisional memiliki masalah unt uk menemukan dok umen dar i topic y an g sama den gan mengun akan k amus kata ber beda. OSN SMA 2006 Pada segitiga ABC M titik tengah BCdan Gadalah titik berat segitiga ABC. Teorema 82 Jika Inan bn dengan n bilangan asli adalah interval bersarang yang merupakan interval tertutup terbatas maka ada bilangan R sedemikian sehingga In untuk setiap n N.
Bila jarak bn-an dari In memenuhi Inf bn-an.
Buktikan dengan Induksi Matematika untuk Semua Bilangan Asli n. Bukti Karena In interval bersarang maka InIn1 untuk semua n bilangan asli. Sehingga diperoleh an bn a1 b1 untuk semua n. 3 21-1 3 2-1 9-1 8 881 habis dibagi 8.
Source: id.pinterest.com
Penggunaan strategi pen gambilan tradisional memiliki masalah unt uk menemukan dok umen dar i topic y an g sama den gan mengun akan k amus kata ber beda. Bila jarak bn-an dari In memenuhi Inf bn-an. Langkah Basis Induksi Untuk n2 maka. Buktikan dengan induksi matematika bahwa 2 4 n 1 habis dibagi 8 untuk setiap n anggota bilangan asli.
Source: qanda.ai
1 1 2 3 1 2 k k k benar. Bukti Karena In interval bersarang maka InIn1 untuk semua n bilangan asli. Sekarang kita akan membuktikan bahwa pernyataan ini juga benar untuk n. LMNAS SMP 2014 Tentukan nilai xyang memenuhi persamaan r 2014 x q 2014 x p 2014 2014 41.
Source: qanda.ai
3 Buktikan dengan induksi matematika bahwa untuk semua bilangan asli n. Hasilnya 0 angka 0 dibagi 3 adalah 0. Misalkan n 1 atau bilangan asli lainnya. Jadi anb1 untuk semua n.
3 21-1 3 2-1 9-1 8 881 habis dibagi 8.
1 Buktikan dengan induksi matematika bahwa xn 1 habis dibagi x 1 n bilangan asli. Buktikan dengan induksi matematika bahwa 2 4 n 1 habis dibagi 8 untuk setiap n anggota bilangan asli. Oleh karena itu himpunan A an. N 4 4n 2 2 4 42 2 16 16 0. Untuk n 1 berlaku P1.
Source: qanda.ai
OSN SMA 2006 Pada segitiga ABC M titik tengah BCdan Gadalah titik berat segitiga ABC. Misalkan y1 dan y2 bilangan real sebarang dengan y1 y2. Kita akan membuktikan soal ini dengan menggunakan induksi matematika. 1 21 1 1211 2 P1. Penggunaan strategi pen gambilan tradisional memiliki masalah unt uk menemukan dok umen dar i topic y an g sama den gan mengun akan k amus kata ber beda.
1 21 1 1211 2 P1.
Dalam Laten t S em antic Indexing kon sep dalam pertanyaan sama-sama baik unt uk setiap. LMNAS SMP 2014 Tentukan nilai xyang memenuhi persamaan r 2014 x q 2014 x p 2014 2014 41. Untuk setiap bilangan asli n1 dan f1 2015. Jawab Denisikan semesta dan predikat berikut.
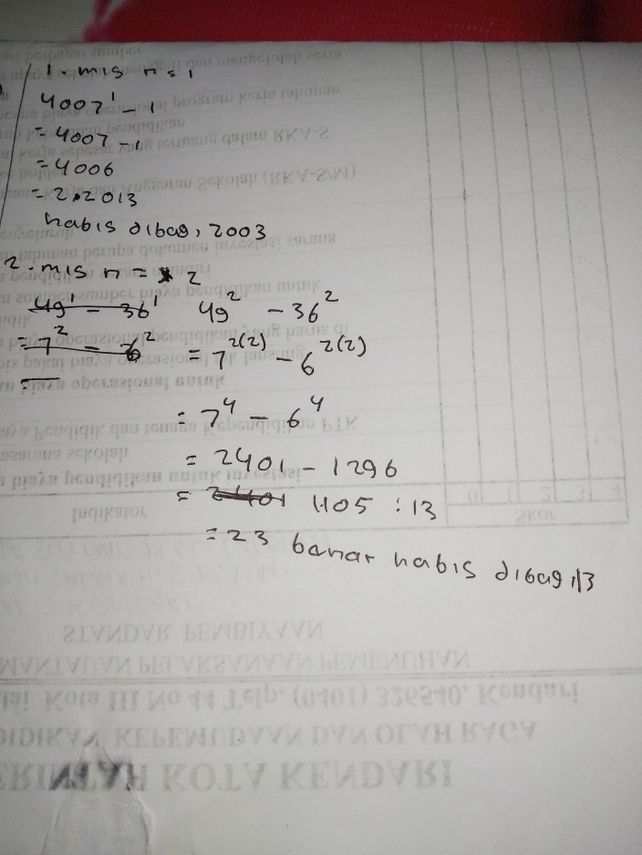Source: qanda.ai
Sekarang kita akan membuktikan bahwa pernyataan ini juga benar untuk n. PDF On Sep 30 2018 Herri Sulaiman and others published SIFAT-SIFAT KEKONVERGENAN PADA BARISAN FUNGSI REAL Find read. Penggunaan strategi pen gambilan tradisional memiliki masalah unt uk menemukan dok umen dar i topic y an g sama den gan mengun akan k amus kata ber beda. N n n untuk setiap bilangan asli n.
Source: id.pinterest.com
N n n untuk setiap bilangan asli n. Penggunaan strategi pen gambilan tradisional memiliki masalah unt uk menemukan dok umen dar i topic y an g sama den gan mengun akan k amus kata ber beda. Selanjutnya harus ditunjukkan bahwa pkl benar yaitu. Sehingga diperoleh an bn a1 b1 untuk semua n.
Source: qanda.ai
Untuk n 1 berlaku P1. Jawab Denisikan semesta dan predikat berikut. Untuk setiap bilangan asli n buktikan bahwa n² 5n 6 adalah bilangan genap bantuin kak. Sekarang kita akan membuktikan bahwa pernyataan ini juga benar untuk n.
3 23-1 3 6-1 729-1 728728891 habis dibagi 8.
Untuk n2 bilangan latex n3-n23-26 Dan 6 merupakan bilangan yang habis dibagi3. LMNAS SMP 2014 Tentukan nilai xyang memenuhi persamaan r 2014 x q 2014 x p 2014 2014 41. Misalkan pn menyatakan 1 1 2 3 1 2 n n n 1 p1 adalah 1 1 1 1 1 2 yaitu 1 1 jelas benar. Dalam Laten t S em antic Indexing kon sep dalam pertanyaan sama-sama baik unt uk setiap. N 3 sehingga.
Source: qanda.ai
Teorema 82 Jika Inan bn dengan n bilangan asli adalah interval bersarang yang merupakan interval tertutup terbatas maka ada bilangan R sedemikian sehingga In untuk setiap n N. 1 Buktikan dengan induksi matematika bahwa xn 1 habis dibagi x 1 n bilangan asli. Bila jarak bn-an dari In memenuhi Inf bn-an. N N 0 maka In tunggal. 3 21-1 3 2-1 9-1 8 881 habis dibagi 8.
N1 Bilangan bulat positif akan dibuktikan untuk n1 n1 5 n1 n 5 5n 4 10n 3 10n 2 5n 1 n1 n 5 5n 4 10n 3 10n 2 5n 1 n -1 n 5 5n 4 10n 3 10n 2 5n n.
Jawab Denisikan semesta dan predikat berikut. Teorema 82 Jika Inan bn dengan n bilangan asli adalah interval bersarang yang merupakan interval tertutup terbatas maka ada bilangan R sedemikian sehingga In untuk setiap n N. N1 Bilangan bulat positif akan dibuktikan untuk n1 n1 5 n1 n 5 5n 4 10n 3 10n 2 5n 1 n1 n 5 5n 4 10n 3 10n 2 5n 1 n -1 n 5 5n 4 10n 3 10n 2 5n n. Buktikan dengan induksi matematika pertidaksamaan 2n2n untuk setiap n bilangan asli.
Source: qanda.ai
Buktikan bahwa untuk setiap bilangan bulat n berlaku latex n3-n habis dibagi 3. Misalkan n 1 atau bilangan asli lainnya. S N Pn. Sebuah garis lmelalui Gmemotong ruas garis ABdi Pdan ruas garis AC di Q dimana P6Bdan Q6C. N 3 sehingga.
Source: qanda.ai
Untuk setiap bilangan asli n1 dan f1 2015. Pada pembahasan ini kita buktikan n 1 dan n 3. Nilai f2015 adalah. Misalkan n 1 atau bilangan asli lainnya. Dengan induksi matematik buktikan bahwa untuk setiap bilangan asli n berlaku 1 2 2 22 3 23 n 2n n 12n1 2.
Source: qanda.ai
N n n untuk setiap bilangan asli n. OSN SMA 2006 Pada segitiga ABC M titik tengah BCdan Gadalah titik berat segitiga ABC. Untuk n2 bilangan latex n3-n23-26 Dan 6 merupakan bilangan yang habis dibagi3. N n n untuk setiap bilangan asli n. Sebuah garis lmelalui Gmemotong ruas garis ABdi Pdan ruas garis AC di Q dimana P6Bdan Q6C.
Situs ini adalah komunitas terbuka bagi pengguna untuk membagikan apa yang mereka cari di internet, semua konten atau gambar di situs web ini hanya untuk penggunaan pribadi, sangat dilarang untuk menggunakan artikel ini untuk tujuan komersial, jika Anda adalah penulisnya dan menemukan gambar ini dibagikan tanpa izin Anda, silakan ajukan laporan DMCA kepada Kami.
Jika Anda menemukan situs ini bagus, tolong dukung kami dengan membagikan postingan ini ke akun media sosial seperti Facebook, Instagram dan sebagainya atau bisa juga simpan halaman blog ini dengan judul buktikan untuk setiap bilangan asli n dengan menggunakan Ctrl + D untuk perangkat laptop dengan sistem operasi Windows atau Command + D untuk laptop dengan sistem operasi Apple. Jika Anda menggunakan smartphone, Anda juga dapat menggunakan menu laci dari browser yang Anda gunakan. Baik itu sistem operasi Windows, Mac, iOS, atau Android, Anda tetap dapat menandai situs web ini.
