Rumus suku ke n dari barisan bilangan.
Jika kamu mencari artikel rumus suku ke n dari barisan bilangan terlengkap, berarti kamu sudah berada di website yang tepat. Yuk langsung aja kita simak penjelasan rumus suku ke n dari barisan bilangan berikut ini.
1 From encrypted-tbn0.gstatic.com
Sementara itu barisan polinom berderajat 2 adalah barisan polinom dengan rumus suku ke-n yang dapat ditulis dalam bentuk un an2 bn c dengan n adalah variabelnya peubahnya dan a b c adalah konstantanya. Bilangan pertama atau suku pertama dilambangkan dengan u 1 suku kedua dengan u 2 suku ketiga dengan u 3 suku ke-k dengan u k dan suku ke n dengan u n. Rumus Deret Aritmatika Barisan dari aritmatika dapat di artikan yang artinya adalah susunan bilangan yang real dan membentuk pola tertentu. Bilangan-bilangan yang membentuk barisan disebut suku-suku barisan.
Dari barisan bilangan di atas tentuka.
Contoh Soal 7 13 19 25 31 37. Dalam hal ini kita membagi kasus berdasarkan sisa pembagian oleh. Bilangan-bilangan yang membentuk barisan disebut suku-suku barisan. Un Un-1 Un-2. U 2 suku ke-2 8 U 4 suku ke-4 32 Suku ke-n U n dari suatu barisan bilangan dapat ditentukan apabila telah diketahui paling sedikit tiga buah suku.
Source: qanda.ai
Jadi diperoleh Rumus barisan aritmatika sebagai berikut. Misalnya menentukan suku ke n dari barisan bilangan. - Bentuk pertanyaan Tentukan rumus suku ke-n dari setiap barisan bilangan berikuta. Rumus Suku ke-n Un Barisan aritmatika terdiri dari beberapa suku yang diurutkan dari kiri ke kanan dengan beda yang sama untuk setiap dua suku yang berdekatan. Dengan seperlunya menambahkan beberapa suku berikutnya kita dapat menganggap bahwa barisan di atas bersifat periodik dengan periode minimal untuk setiap bilangan asli.
Sn n2 aUn a Suku Pertama.
A suku pertama. Sementara itu barisan polinom berderajat 2 adalah barisan polinom dengan rumus suku ke-n yang dapat ditulis dalam bentuk un an2 bn c dengan n adalah variabelnya peubahnya dan a b c adalah konstantanya. Dalam hal ini kita membagi kasus berdasarkan sisa pembagian oleh. Suku ke-n suatu barisan bilangan dilmabangkan dengan U n.
Source: youtube.com
Kemudian arti dari deret aritmatika sendiri iyalah sebuah penjumlahan dari barisan aritmatika. Sn n2 aUn a Suku Pertama. A suku pertama. Jadi diperoleh Rumus barisan aritmatika sebagai berikut.
Source: catatanmatematika.com
B beda selisih n banyaknya suku. Beda b U2 U1 U3 U2 dst. Diketahui barisan bilangan 4 8 16 32 64. Kemudian arti dari deret aritmatika sendiri iyalah sebuah penjumlahan dari barisan aritmatika.
Source: qanda.ai
B rasio atau beda. Nilai dari a 4 Un a n-1b Un 4 n-1-2 Un 4 -2n 2 Un 6 2n Jadi rumus untuk mengetahui suku ke n adalah Un 6 2n. Untuk itu diperlukan cara untuk menentukan suku ke-n dari suatu barisan. Rumus Suku ke-n.
Bilangan-bilangan yang membentuk barisan disebut suku-suku barisan. A suku pertama. - Bentuk pertanyaan Tentukan rumus suku ke-n dari setiap barisan bilangan berikuta. Suku ke-n Suku ke-n dari suatu bilangan sebanyak k suku pertama diperoleh banyak kemungkinan rumus suku ke n.
B rasio atau beda.
B rasio atau beda. Dengan b adalah beda barisan atau selisih antar dua suku yang berdekatan Un suku ke-n suatu barisan n 1 2 3 dan U n-1 adalah suku terdekat sebelum Un. Tentukan suku ke-2 U 2 dan suku ke-4 U 4. - Bentuk pertanyaan Tentukan rumus suku ke-n dari setiap barisan bilangan berikuta. Barisan polinom berderajat 1 adalah barisan polinom dengan rumus suku ke-n un yang dapat ditulis dalam bentuk un an b.
Source: id.pinterest.com
Dari barisan 48 24 12. Rumus Suku ke-n. Dalam hal ini kita membagi kasus berdasarkan sisa pembagian oleh. Jumlah n suku pertama. Suku ke-n suatu barisan bilangan dilmabangkan dengan U n.
N bilangan asli Indeks n menyatakan banyaknya suku dalam barisan itu. - Bentuk pertanyaan Tentukan rumus suku ke-n dari setiap barisan bilangan berikuta. Rumus Deret Aritmatika Barisan dari aritmatika dapat di artikan yang artinya adalah susunan bilangan yang real dan membentuk pola tertentu. Andaikan suku ke empat adalah 16 mungkin Un 2n Andaikan suku ke empat adalah 14 mungkin Un n2 n 2.
B rasio atau beda.
Tentukan suku ke-2 U 2 dan suku ke-4 U 4. Berapa rumus untuk mencari suku ke n. Barisan Aritmatika adalah barisan bilangan dimana suku selanjutnya diperoleh dari menjumlahkan bilangan tetap terhadap suku sebelumnya. - Lihat pembahasan yang l.
Source: qanda.ai
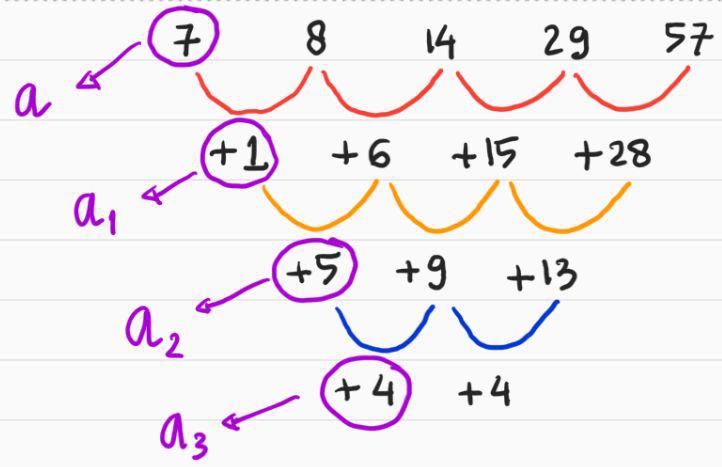
Rumus suku ke- dari barisan ini dapat dituliskan dalam bentuk bercabang seperti di paragraf sebelumnya. Kemudian arti dari deret aritmatika sendiri iyalah sebuah penjumlahan dari barisan aritmatika. B beda selisih n banyaknya suku. Dengan seperlunya menambahkan beberapa suku berikutnya kita dapat menganggap bahwa barisan di atas bersifat periodik dengan periode minimal untuk setiap bilangan asli.
Source: brainly.co.id
Sementara itu barisan polinom berderajat 2 adalah barisan polinom dengan rumus suku ke-n yang dapat ditulis dalam bentuk un an2 bn c dengan n adalah variabelnya peubahnya dan a b c adalah konstantanya. Jumlah n suku pertama. Diketahui barisan bilangan 4 8 16 32 64. Jadi diperoleh Rumus barisan aritmatika sebagai berikut.
Source: ruangguru.com
Dari barisan bilangan di atas tentuka. Beda b U2 U1 U3 U2 dst. Dengan b adalah beda barisan atau selisih antar dua suku yang berdekatan Un suku ke-n suatu barisan n 1 2 3 dan U n-1 adalah suku terdekat sebelum Un. B beda selisih n banyaknya suku.
Dalam hal ini kita membagi kasus berdasarkan sisa pembagian oleh.
Untuk itu diperlukan cara untuk menentukan suku ke-n dari suatu barisan. Tentukan suku ke-2 U 2 dan suku ke-4 U 4. - Lihat pembahasan yang l. Bilangan pertama atau suku pertama dilambangkan dengan u 1 suku kedua dengan u 2 suku ketiga dengan u 3 suku ke-k dengan u k dan suku ke n dengan u n. Rumus suku ke- dari barisan ini dapat dituliskan dalam bentuk bercabang seperti di paragraf sebelumnya.
Source: brainly.co.id
Contoh Soal 7 13 19 25 31 37. U 2 suku ke-2 8 U 4 suku ke-4 32 Suku ke-n U n dari suatu barisan bilangan dapat ditentukan apabila telah diketahui paling sedikit tiga buah suku. Rumus Suku ke-n Un Barisan aritmatika terdiri dari beberapa suku yang diurutkan dari kiri ke kanan dengan beda yang sama untuk setiap dua suku yang berdekatan. Dalam hal ini kita membagi kasus berdasarkan sisa pembagian oleh. Un Un-1 Un-2.
Jumlah n suku pertama.
Suku ke-n Suku ke-n dari suatu bilangan sebanyak k suku pertama diperoleh banyak kemungkinan rumus suku ke n. Dari barisan bilangan di atas tentuka. Dalam hal ini kita membagi kasus berdasarkan sisa pembagian oleh. Untuk itu diperlukan cara untuk menentukan suku ke-n dari suatu barisan.
Source: slideshare.net
N banyaknya suku. Dari barisan 48 24 12. Misalnya menentukan suku ke n dari barisan bilangan. Tentukan rumus suku ke n dari barisan tersebut.
Source: caraharian.com
Un suku ke n. Misalnya menentukan suku ke n dari barisan bilangan. Dengan seperlunya menambahkan beberapa suku berikutnya kita dapat menganggap bahwa barisan di atas bersifat periodik dengan periode minimal untuk setiap bilangan asli. N bilangan asli Indeks n menyatakan banyaknya suku dalam barisan itu.
Source: qanda.ai
Rumus Suku ke-n. Untuk itu diperlukan cara untuk menentukan suku ke-n dari suatu barisan. Un a n-1b. Misalnya menentukan suku ke n dari barisan bilangan.
Sn n2 aUn a Suku Pertama.
N banyaknya suku. Tentukan rumus suku ke n dari barisan tersebut. N banyaknya suku. Un suku ke n. Rumus Barisan Aritmatika Un a n 1 b b Un -Un-1 atau b Un1 Un Keterangan.
Source: ruangguru.com
Sn n2 aUn a Suku Pertama. Rumus suku ke-n dari barisan aritmetika Untuk menentukan suku ke-n suatu barisan bilangan aritmetika dimana n relatif besar tentunya akan sulit jika kita harus menuliskan seluruh anggota barisan bilangan tersebut. Bilangan pertama atau suku pertama dilambangkan dengan u 1 suku kedua dengan u 2 suku ketiga dengan u 3 suku ke-k dengan u k dan suku ke n dengan u n. 2 4 0 2 -2 0 -2 Suku ke -1 adalah 4. U 2 suku ke-2 8 U 4 suku ke-4 32 Suku ke-n U n dari suatu barisan bilangan dapat ditentukan apabila telah diketahui paling sedikit tiga buah suku.
Bilangan-bilangan yang membentuk barisan disebut suku-suku barisan.
Berdasarkan uraian pada bab sebelumnya dapat diambil kesimpulan bahwa metode persamaan karakteristik memberikan perolehan bentuk umum rumus suku ke-n barisan bilangan lebih mudah bila dibandingkan dengan menggunakan metode fungsi pembangkit yang memberikan hasil yang sama dari sebuah relasi rekurensi yang berbentuk. Tentukan rumus suku ke n dari barisan tersebut. Tentukan suku ke-2 U 2 dan suku ke-4 U 4. Rumus Suku ke-n Un Barisan aritmatika terdiri dari beberapa suku yang diurutkan dari kiri ke kanan dengan beda yang sama untuk setiap dua suku yang berdekatan.
Source: ruangguru.com
Akan tetapi bila anda diminta menentukan suku ke-100 dari barisan bilangan genap. A suku pertama. Suku ke-n suatu barisan bilangan dilmabangkan dengan U n. Un a n-1b. N banyaknya suku.
Source: brainly.co.id
Rumus suku ke-n dari barisan aritmetika Untuk menentukan suku ke-n suatu barisan bilangan aritmetika dimana n relatif besar tentunya akan sulit jika kita harus menuliskan seluruh anggota barisan bilangan tersebut. Un suku ke n. Rumus Suku ke-n. Berapa rumus untuk mencari suku ke n. Dengan seperlunya menambahkan beberapa suku berikutnya kita dapat menganggap bahwa barisan di atas bersifat periodik dengan periode minimal untuk setiap bilangan asli.
Source: qanda.ai
Rumus Deret Aritmatika Barisan dari aritmatika dapat di artikan yang artinya adalah susunan bilangan yang real dan membentuk pola tertentu. Rumus suku ke-n barisan aritmetika Jika anda diminta menentukan suku ke-100 dari barisan bilangan asli tentu saja anda dengan mudahnya dapat menjawab pertanyaan tersebut. Contoh Soal 7 13 19 25 31 37. Bilangan pertama atau suku pertama dilambangkan dengan u 1 suku kedua dengan u 2 suku ketiga dengan u 3 suku ke-k dengan u k dan suku ke n dengan u n. 2 4 0 2 -2 0 -2 Suku ke -1 adalah 4.
Situs ini adalah komunitas terbuka bagi pengguna untuk berbagi apa yang mereka cari di internet, semua konten atau gambar di situs web ini hanya untuk penggunaan pribadi, sangat dilarang untuk menggunakan artikel ini untuk tujuan komersial, jika Anda adalah penulisnya dan menemukan gambar ini dibagikan tanpa izin Anda, silakan ajukan laporan DMCA kepada Kami.
Jika Anda menemukan situs ini baik, tolong dukung kami dengan membagikan postingan ini ke akun media sosial seperti Facebook, Instagram dan sebagainya atau bisa juga simpan halaman blog ini dengan judul rumus suku ke n dari barisan bilangan dengan menggunakan Ctrl + D untuk perangkat laptop dengan sistem operasi Windows atau Command + D untuk laptop dengan sistem operasi Apple. Jika Anda menggunakan smartphone, Anda juga dapat menggunakan menu laci dari browser yang Anda gunakan. Baik itu sistem operasi Windows, Mac, iOS, atau Android, Anda tetap dapat menandai situs web ini.
